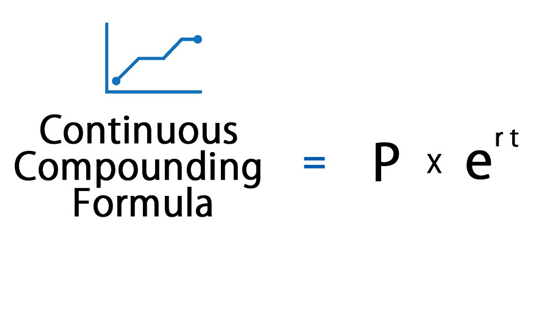निरंतर कम्पाउंडिंग म्हणजे काय?

परिचय

अर्थव्यवस्थेला चालविण्यासाठी महत्त्वाचे असलेल्या व्याज दरांची गणना करण्यासाठी सतत कम्पाउंडिंगची आवश्यकता आहे. लोक एफडी अकाउंट उघडण्यापूर्वी किंवा कोणत्याही पोर्टफोलिओमध्ये इन्व्हेस्टमेंट करण्यापूर्वी इंटरेस्ट टक्केवारी शोधतात, कारण विविध मार्गांनी इंटरेस्ट रेटची गणना केली जाते. व्याज कॅल्क्युलेट करण्याचे एक मार्ग हे निरंतर कम्पाउंडिंगद्वारे आहे. या लेखात, चला सतत कम्पाउंडिंग म्हणजे काय आणि तुम्ही त्याची गणना कशी करू शकता हे समजूया.

निरंतर कम्पाउंडिंग म्हणजे काय?

निरंतर कम्पाउंडिंग ही कम्पाउंड इंटरेस्ट कॅल्क्युलेशनची मर्यादा आहे जिथे इंटरेस्ट अकाउंटच्या बॅलन्समध्ये अनंत वेळा पुन्हा इन्व्हेस्ट केला जातो. हे संपूर्ण इन्व्हेस्टमेंटच्या इंटरेस्ट घटक आणि पोर्टफोलिओचे मूल्य वाढवते. जरी ते वास्तविक जगात व्यावहारिक नसेल तरीही ते आर्थिक जगात आवश्यक आहे. 

याव्यतिरिक्त, हे एक स्पोरॅडिक कम्पाउंडिंग केस आहे कारण बहुतेक प्राप्त व्याज मासिक, तिमाही, अर्ध-वार्षिक किंवा वार्षिक संयुक्त केले जाते. सोप्या शब्दांमध्ये, सतत कम्पाउंडिंग असे गृहीत धरते की व्याज एकत्रित केले जाते आणि स्त्रोत अकाउंटमध्ये पुन्हा अनंत वेळा जोडले जाते. याचा अर्थ असा की अकाउंट नियमितपणे व्याज कमावत आहे, बॅलन्समध्ये समान व्याज परत इन्व्हेस्ट करत आहे आणि त्यावर पुन्हा व्याज कमवत आहे.

निरंतर कम्पाउंडिंगचे महत्त्व

निरंतर कम्पाउंडिंग का आवश्यक आहे याची काही कारणे येथे दिली आहेत:

1. व्याज जमा झाल्यावर किती शिल्लक मिळू शकते हे दर्शविते.
2. इन्व्हेस्टरना त्यांच्या इन्व्हेस्टमेंटमधून किती अपेक्षा करू शकतात हे कॅल्क्युलेट करण्यास मदत करते, सतत कम्पाउंडिंग इंटरेस्ट कमवते.
3. हे इन्व्हेस्टरना अधिक नफा मिळविण्यासाठी हे कमावलेले व्याज कुठे पुन्हा इन्व्हेस्ट करावे याचा चांगला निर्णय घेण्यास मदत करते.
4. ही साध्या व्याजापेक्षा जलद रक्कम वाढवते, कारण नंतरची रक्कम केवळ मुख्य रकमेवर मोजली जाते.
5. कम्पाउंडिंगद्वारे, पैसे वाढलेल्या दराने गुणवत्ता केले जातात. कम्पाउंडिंग कालावधी जास्त असल्यास, अधिक कम्पाउंड इंटरेस्ट असेल.
6. हे विशेषत: दीर्घकाळात इन्व्हेस्टमेंट रिटर्न देखील वाढवू शकते.

निरंतर कम्पाउंडिंग फॉर्म्युला

आता जेव्हा तुम्ही निरंतर कम्पाउंडिंग अर्थ समजला आहे, तेव्हा त्याच्या फॉर्म्युला पाहण्याची वेळ आली आहे. खाली सातत्याने कम्पाउंड केलेला फॉर्म्युला आहे:
A= पर्ट
 

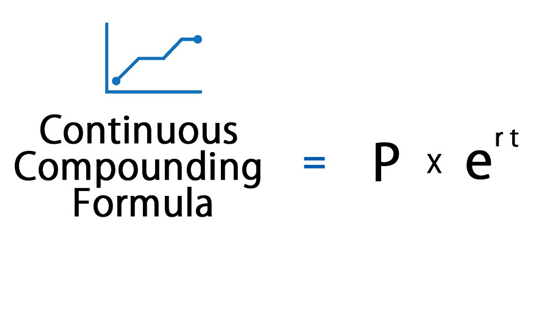
कम्पाउंडिंग फॉर्म्युलाची गणना

येथे या विभागात, सलग कम्पाउंड इंटरेस्ट फॉर्म्युलाचे विविध घटक समजून घेऊया:
A= पर्ट 

वरीलमध्ये,

A = अंतिम रक्कम
P = प्रारंभिक रक्कम
R = इंटरेस्ट रेट
t = वेळ 
ई = गणितीय सातत्यपूर्ण, जेथे ई = 2.7183

या गणनेमध्ये, ते कम्पाउंड करण्याची योजना कशी आहे यावर वेळ बदलते. जर तिमाही असेल तर वेळ 1/4th असेल. 

जर तो द्वि-वार्षिक केला असेल तर वेळ 1/2th असेल; जर ते वार्षिकरित्या केले असेल तर ते 1/365 असेल. 

कॅल्क्युलेशन तासातून, मिनिट किंवा दैनंदिन आधारावरही होऊ शकते. आणि व्यावहारिक अटींमध्ये, ते कोणतेही मूल्य बनवत नाही कारण फक्त दशांश बिंदूमध्ये असेल. 

निरंतर कम्पाउंडिंग फॉर्म्युला कसा प्राप्त करावा?

कंपाउंड इंटरेस्ट फॉर्म्युला मधून निरंतर कम्पाउंडिंग फॉर्म्युला प्राप्त केला जातो. कम्पाउंड इंटरेस्ट फॉर्म्युला खालीलप्रमाणे आहे:
A = P (1 + r/n)nt

वरीलमध्ये,

A = अंतिम रक्कम किंवा भविष्यातील मूल्य म्हणूनही ओळखली जाऊ शकते
P = प्रारंभिक रक्कम
N = ही काळाची संख्या आहे किंवा प्रारंभिक रक्कम कम्पाउंडिंग आहे
t = वेळ
r = इंटरेस्ट रेट

निरंतर कम्पाउंड इंटरेस्टच्या बाबतीत, n →. त्यामुळे, वरील फॉर्म्युलामधील मर्यादा आहे 
A = LIMNNT → P (1 + r/n)nt = पर्ट

नंतर, अंतिम स्टेपमध्ये, मर्यादा फॉर्म्युलापैकी एक वापरले जाते: limn→ (1 + r/n)n = er.

आणि तेथून निरंतर कम्पाउंडिंग फॉर्म्युला प्राप्त केला जातो, जे  

A= पर्ट

निरंतर कम्पाउंडिंग कसे वापरावे याची उदाहरणे
उदाहरणाच्या मदतीने फॉर्म्युला वापरून समजून घेऊया. 

उदाहरणार्थ: बँकेत जमा केलेली प्रारंभिक रक्कम व्याज दरावर ₹2340 आहे: वार्षिक आधारावर 3.1%. तीन (3) वर्षांनंतर बॅलन्स काय असेल?

त्यामुळे, फॉर्म्युला म्हणतात, A= पर्ट

वरील उदाहरणातून, P = 2340, 
आर = 3.1, जे 3.1/100 = 0.031 असेल
 t = 3 (आम्हाला 3 वर्षांसाठी कॅल्क्युलेट करणे आवश्यक असल्याने)
ई = नेपियर्स क्रमांक, जे अंदाजे 2.7183 आहे

चला कॅल्क्युलेट करूयात:
A = 2340 e0.031(3) C 2568.06

त्यामुळे, तीन वर्षांनंतर, प्राप्त झालेली रक्कम ₹2568.05 असेल

साधारण इंटरेस्ट विरुद्ध कम्पाउंड इंटरेस्ट
या दोघांची गणना कशी केली जाते यामध्ये फरक आहे. 

एका निश्चित कालावधीनंतर प्रारंभिक मुद्दल रकमेवर प्राप्त झालेले व्याज हे सोपे व्याज आहे. अशा प्रकरणांमध्ये, व्याज प्रारंभिक रकमेमध्ये जोडलेले नाही. व्याज विशिष्ट वेळी प्रारंभिक रकमेवर दिला जातो. 

दुसऱ्या बाजूला, कम्पाउंड इंटरेस्टमध्ये, प्रारंभिक मुख्य रक्कम कमावलेले व्याज समायोजित करण्यासाठी बदलते. त्यामुळे प्रत्येक वर्षी, तुम्हाला प्राप्त होणारी रक्कम आरंभिक मूळ रकमेमध्ये जोडलेले मागील वर्षाचे व्याज असेल.

निष्कर्ष

फॉर्म्युला सुरुवातीच्या मुख्य रकमेवर कमवलेले व्याज तपासते. या प्रकरणात, कम्पाउंडिंग वेळ अनेकदा अनंत मानली जाते. सातत्यपूर्ण कम्पाउंडिंगमध्ये रकमेचे अंतिम मूल्य साधारण व्याजापेक्षा जास्त असल्याचे दर्शविले तरीही, वास्तविक जगभरात अर्ज करणे आव्हानकारक आहे. म्हणूनच, वास्तविक जीवनात वापरणे खूपच व्यावहारिक असू शकत नाही कारण ते आर्थिक जगात महत्त्वपूर्ण आहे. 

त्याऐवजी, ते इन्व्हेस्टरच्या बाजूने मूल्य धारण करते. गुंतवणूकदार 'X' गुंतवणूकीवर प्राप्त होणारी रक्कम तपासू शकतात आणि भविष्यातील गुंतवणूक योजनांवर निर्णय घेऊ शकतात.