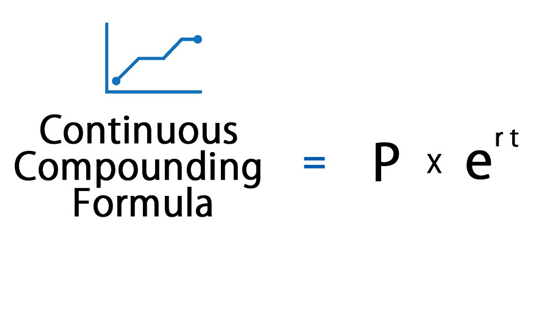સતત કમ્પાઉન્ડિંગ શું છે?

પરિચય

વ્યાજના દરોની ગણતરી કરવા માટે સતત કમ્પાઉન્ડિંગની જરૂર છે, જે અર્થવ્યવસ્થા ચલાવવા માટે નિર્ણાયક છે. લોકો એફડી એકાઉન્ટ ખોલતા પહેલાં અથવા કોઈપણ પોર્ટફોલિયોમાં ઇન્વેસ્ટ કરતા પહેલાં વ્યાજની ટકાવારી શોધે છે, કારણ કે વ્યાજનો દરની ગણતરી વિવિધ રીતોનો ઉપયોગ કરીને કરવામાં આવે છે. વ્યાજની ગણતરી કરવાની એક રીત સતત કમ્પાઉન્ડિંગ દ્વારા છે. આ લેખમાં, ચાલો સમજીએ કે સતત કમ્પાઉન્ડિંગ શું છે અને તમે તેની ગણતરી કેવી રીતે કરી શકો છો.

સતત કમ્પાઉન્ડિંગ શું છે?

સતત કમ્પાઉન્ડિંગ એ કમ્પાઉન્ડ વ્યાજની ગણતરીની મર્યાદા છે જ્યાં વ્યાજને એકાઉન્ટના બૅલેન્સમાં અનન્ય વખત ફરીથી રોકાણ કરવામાં આવે છે. તે વ્યાજનો ઘટક અને સંપૂર્ણ રોકાણના પોર્ટફોલિયોનું મૂલ્ય વધારે છે. જોકે તે વાસ્તવિક દુનિયામાં વ્યવહારુ ન હોઈ શકે, પરંતુ તે ફાઇનાન્શિયલ દુનિયામાં આવશ્યક છે. 

વધુમાં, તે એક સ્પોરેડિક કમ્પાઉન્ડિંગ કેસ છે કારણ કે મોટાભાગના પ્રાપ્ત વ્યાજ માસિક, ત્રિમાસિક, અર્ધ-વાર્ષિક અથવા વાર્ષિક રૂપે કમ્પાઉન્ડ કરવામાં આવે છે. સરળ શબ્દોમાં, સતત કમ્પાઉન્ડિંગ ધારણ કરે છે કે વ્યાજ કમ્પાઉન્ડ કરવામાં આવે છે અને સ્રોત એકાઉન્ટમાં અસંખ્ય વખત ઉમેરવામાં આવે છે. તેનો અર્થ એ છે કે એકાઉન્ટ નિયમિતપણે વ્યાજ કમાઈ રહ્યું છે, બૅલેન્સમાં સમાન વ્યાજનું ફરીથી ઇન્વેસ્ટ કરી રહ્યું છે, અને ફરીથી તેના પર વ્યાજ કમાઈ રહ્યું છે.

સતત કમ્પાઉન્ડિંગનું મહત્વ

સતત કમ્પાઉન્ડિંગ શા માટે જરૂરી છે તેના કેટલાક કારણો અહીં આપેલ છે:

1. જ્યારે વ્યાજ પ્રાપ્ત થઈ રહ્યું હોય ત્યારે કેટલું બૅલેન્સ કમાઈ શકાય છે તે દર્શાવે છે.
2. તે રોકાણકારોને તેમના રોકાણથી કેટલી અપેક્ષા રાખી શકે છે તેની ગણતરી કરવામાં મદદ કરે છે, અને સતત કમ્પાઉન્ડિંગ વ્યાજ મેળવે છે.
3. તે રોકાણકારોને વધુ નફો મેળવવા માટે આ કમાયેલા વ્યાજને ક્યાં ફરીથી રોકાણ કરવાનો એક મજબૂત નિર્ણય લેવામાં મદદ કરે છે.
4. તે સરળ વ્યાજ કરતાં ઝડપી રકમ વધારે છે, કારણ કે પછીની રકમની ગણતરી માત્ર મૂળ રકમ પર કરવામાં આવે છે.
5. કમ્પાઉન્ડિંગ દ્વારા, પૈસા વધારેલા દરે ગુણાકાર કરવામાં આવે છે. કમ્પાઉન્ડિંગ સમયગાળા જેટલી વધુ હશે, તેટલું વધુ કમ્પાઉન્ડ વ્યાજ હશે.
6. તે રોકાણના વળતરને પણ વધારી શકે છે, ખાસ કરીને લાંબા ગાળે.

સતત કમ્પાઉન્ડિંગ ફોર્મ્યુલા

હવે તમે સતત કમ્પાઉન્ડિંગનો અર્થ સમજી લીધો છે, તેના ફોર્મ્યુલાને જોવાનો સમય આવી ગયો છે. નીચે કમ્પાઉન્ડ કરેલ સતત ફોર્મ્યુલા છે:
A= પર્ટ
 

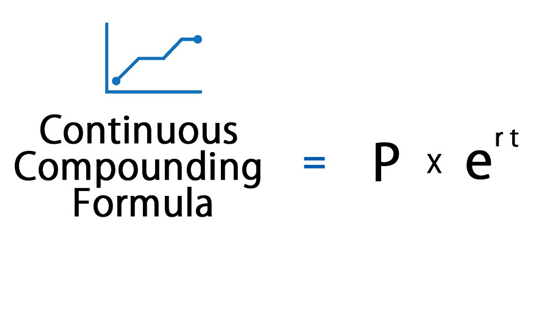
કમ્પાઉન્ડિંગ ફોર્મ્યુલાની ગણતરી

અહીં આ વિભાગમાં, ચાલો સતત કમ્પાઉન્ડ વ્યાજ ફોર્મ્યુલાના વિવિધ તત્વોને સમજીએ:
A= પર્ટ 

ઉપરોક્તમાં,

A = અંતિમ રકમ
P = પ્રારંભિક રકમ
R = વ્યાજ દર
t = સમય
E = ગણિત સ્થિર, જ્યાં E = 2.7183

આ ગણતરીમાં, તેને કેવી રીતે કમ્પાઉન્ડ કરવાની યોજના બનાવવામાં આવે છે તેના પર સમય બદલાય છે. જો તે ત્રિમાસિક હોય, તો સમય 1/4th રહેશે. 

જો તે દ્વિ-વાર્ષિક રીતે કરવામાં આવે છે, તો સમય 1/2th રહેશે; જો તે વાર્ષિક ધોરણે કરવામાં આવે છે, તો તે 1/365 હશે. 

ગણતરી કલાક, મિનિટ અથવા દૈનિક ધોરણે પણ થઈ શકે છે. અને વ્યવહારિક શબ્દોમાં, જે કોઈ મૂલ્ય બનાવતું નથી કારણ કે તફાવત માત્ર દશાંશ બિંદુઓમાં રહેશે. 

સતત કમ્પાઉન્ડિંગ ફોર્મ્યુલા કેવી રીતે મેળવવું?

સતત કમ્પાઉન્ડિંગ ફોર્મ્યુલા કમ્પાઉન્ડ વ્યાજ ફોર્મ્યુલામાંથી પ્રાપ્ત કરવામાં આવે છે. કમ્પાઉન્ડ વ્યાજ ફોર્મ્યુલા નીચે મુજબ છે:
A = P (1 + r/n)nt

ઉપરોક્તમાં,

A = અંતિમ રકમ અથવા ભવિષ્યનું મૂલ્ય પણ કહી શકાય છે
P = પ્રારંભિક રકમ
N = તે સમયની P ની સંખ્યા છે અથવા પ્રારંભિક રકમ કમ્પાઉન્ડિંગ છે
t = સમય
R = વ્યાજનો દર

સતત કમ્પાઉન્ડ વ્યાજના કિસ્સામાં, n →. તેથી, ઉપરોક્ત ફોર્મ્યુલાની મર્યાદા છે
A = LimnN0 → P (1 + r/n)nt = Pert

પછી, અંતિમ પગલાંમાં, એક મર્યાદા ફોર્મ્યુલાનો ઉપયોગ કરવામાં આવે છે: limn→ (1 + r/n)n = er.

અને ત્યાંથી, સતત કમ્પાઉન્ડિંગ ફોર્મ્યુલા પ્રાપ્ત કરવામાં આવે છે, જે છે  

A= પર્ટ

સતત કમ્પાઉન્ડિંગનો ઉપયોગ કેવી રીતે કરવો તેના ઉદાહરણો
ચાલો એક ઉદાહરણની મદદથી ફોર્મ્યુલાનો ઉપયોગ કરીને સમજીએ. 

ઉદાહરણ તરીકે: બેંકમાં જમા કરેલી પ્રારંભિક રકમ વ્યાજના દર પર ₹2340 છે: વાર્ષિક ધોરણે 3.1%. ત્રણ (3) વર્ષ પછી કેટલું બૅલેન્સ રહેશે?

તેથી, ફોર્મ્યુલા કહે છે, A= Pert

ઉપરોક્ત ઉદાહરણથી, P = 2340,
આર = 3.1, જે 3.1/100 = 0.031 હશે
t = 3 (કારણ કે અમારે 3 વર્ષ માટે ગણતરી કરવાની જરૂર છે)
e = નેપિયરનો નંબર, જે આશરે 2.7183 છે

ચાલો ગણતરી કરીએ:
A = 2340 e0.031(3) C 2568.06

તેથી, ત્રણ વર્ષ પછી, પ્રાપ્ત થયેલી રકમ ₹2568.05 રહેશે

સરળ વ્યાજ વિરુદ્ધ કમ્પાઉન્ડ વ્યાજ
આ બંનેની ગણતરી કેવી રીતે કરવામાં આવે છે તેમાં તફાવત છે. 

સરળ વ્યાજ એ નિશ્ચિત મુદત પછી પ્રારંભિક મુદ્દલ રકમ પર પ્રાપ્ત વ્યાજ છે. આવા કિસ્સાઓમાં, વ્યાજ પ્રારંભિક રકમમાં ઉમેરવામાં આવતું નથી. વ્યાજની ચુકવણી પ્રારંભિક રકમ પર એક નિર્દિષ્ટ સમયે કરવામાં આવે છે. 

બીજી તરફ, કમ્પાઉન્ડ વ્યાજમાં, પ્રારંભિક મુદ્દલ રકમ કમાયેલ વ્યાજને સમાવવામાં બદલાય છે. તેથી દર વર્ષે, તમને જે રકમ પ્રાપ્ત થશે તે પાછલા વર્ષનું વ્યાજ પ્રારંભિક મૂળ રકમમાં ઉમેરવામાં આવશે.

તારણ

ફોર્મ્યુલા પ્રારંભિક મૂળ રકમ પર કમાયેલ વ્યાજ તપાસે છે. આ કિસ્સામાં, કમ્પાઉન્ડિંગનો સમય ઘણીવાર ઇન્ફિનિટી તરીકે ગણવામાં આવે છે. જોકે સતત કમ્પાઉન્ડિંગ સાધારણ વ્યાજ કરતાં રકમનું અંતિમ મૂલ્ય દર્શાવે છે, પરંતુ વાસ્તવિક વિશ્વના કિસ્સાઓમાં અરજી કરવી પડકારજનક છે. તેથી, વાસ્તવિક જીવનમાં તેનો ઉપયોગ કરવો ખૂબ જ વ્યવહારુ ન હોઈ શકે કારણ કે તે નાણાંકીય દુનિયામાં નોંધપાત્ર મહત્વ ધરાવે છે. 

તેના બદલે, તે રોકાણકારના તરફથી મૂલ્ય ધરાવે છે. રોકાણકારો 'X' રોકાણ પર પ્રાપ્ત થતી રકમ તપાસી શકે છે અને ભવિષ્યના રોકાણ યોજનાઓ પર નક્કી કરી શકે છે.