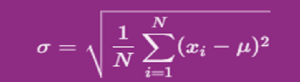स्टँडर्ड डिव्हिएशन

स्टँडर्ड डेव्हिएशन हे एक सांख्यिकीय उपाय आहे जे डाटा मूल्यांच्या संचामध्ये बदल किंवा विस्थापनेची रक्कम मोजते. हे दर्शविते की डाटासेटच्या अर्थ (सरासरी) पेक्षा किती वैयक्तिक डाटा पॉईंट्स भिन्न आहेत. लो स्टँडर्ड डेव्हिएशन हे दर्शविते की डाटा पॉईंट्स अर्थाच्या जवळ आहेत, तर हाय स्टँडर्ड डेव्हिएशन सूचित करते की डाटा विस्तृत श्रेणीमध्ये पसरला जातो. अस्थिरता मूल्यांकन करण्यासाठी, जोखीम अंदाज लावण्यासाठी आणि डाटा वितरण समजून घेण्यासाठी फायनान्स, सायन्स आणि इंजिनीअरिंग सारख्या क्षेत्रांमध्ये स्टँडर्ड डेव्हिएशनचा वापर केला जातो. हे वेरिएंसचे स्क्वेअर रूट आहे, जे स्प्रेडचे अधिक अर्थ लावणारे मोजमाप प्रदान करते.

स्टँडर्ड डेव्हिएशन (एसडी) ही आकडेवारीतील एक मूलभूत संकल्पना आहे जी डाटासेटच्या अर्थ (सरासरी) सभोवतालच्या डाटा पॉईंट्सच्या सेटचे विघटन किंवा प्रसार मोजते. हे आम्हाला डाटामधील फरक समजून घेण्यास मदत करण्यासाठी सरासरी, वैयक्तिक डाटा पॉईंट्सच्या अर्थाने किती दूर आहेत याची भावना देते.

1. स्टँडर्ड डेव्हिएशनसाठी फॉर्म्युला:

लोकसंख्येसाठी (म्हणजेच, संपूर्ण डाटासेट), खालील फॉर्म्युला वापरून स्टँडर्ड डेव्हिएशन कॅल्क्युलेट केले जाते:

कुठे:

• ⁇ लोकसंख्या स्टँडर्ड डेव्हिएशन आहे.
• N ही लोकसंख्येतील डाटा पॉईंट्सची संख्या आहे.
• xi प्रत्येक डाटा पॉईंटचे प्रतिनिधित्व करते.
• ⁇ लोकसंख्या म्हणजे (सरासरी).
• ⁇ सर्व डाटा पॉईंट्सवर रक्कम सूचित करते.

नमुन्यासाठी (म्हणजेच, लोकसंख्येचा उपसेट), फॉर्म्युला लहान आकारासाठी थोडाफार समायोजित केला जातो आणि कमी परिवर्तनीयता टाळतो:

एस=

कुठे:

• एस हा नमुना मानक विचलन आहे.
• n हा नमुनामधील डाटा पॉईंट्सची संख्या आहे.
• X ⁇ हा नमुना अर्थ आहे.

2. स्टँडर्ड डेव्हिएशन कॅल्क्युलेट करण्याच्या स्टेप्स:

1. मान कॅल्क्युलेट करा: डाटासेटची सरासरी शोधा. हे सर्व डाटा पॉईंट्सचा सारांश करून आणि डाटा पॉईंट्सच्या एकूण संख्येद्वारे विभाजित करून केले जाते.

⁇ = ⁇ i^एन = 1 ^xi/एन

मान कडून फरक शोधा: प्रत्येक वॅल्यू याच्या अर्थापासून किती विचलित होते हे निर्धारित करण्यासाठी प्रत्येक डाटा पॉईंटचा अर्थ निकाला.

1. दुरुस्ती स्क्वेअर करा: स्टेप 2 मध्ये प्राप्त केलेल्या प्रत्येक फरक स्क्वेअर करा. ही स्टेप सुनिश्चित करते की नकारात्मक आणि सकारात्मक विचलन एकमेकांना रद्द करत नाही.
2. अत्यंत स्क्वेर्ड फरक: लोकसंख्येसाठी, एनएनएन (डाटा पॉईंट्सची संख्या) द्वारे विभाजित करून या स्क्वेअर्ड फरकांची सरासरी शोधा. नमुन्यासाठी, N--1 द्वारे नमुना आकारासाठी अकाउंटमध्ये विभाजन करा आणि पूर्वग्रह कमी करा.
3. स्क्वेर रुट घ्या: शेवटी, स्टेप 4 पासून परिणामांचे स्क्वेअर रूट घ्या . यामुळे स्टँडर्ड डेव्हिएशन मिळते.

3. इंटरप्रिटिंग स्टँडर्ड डेव्हिएशन:

• कमी स्टँडर्ड डेव्हिएशन: लहान स्टँडर्ड डेव्हिएशन म्हणजे डाटा पॉईंट्स अर्थाच्या जवळ आहेत. डाटा मजबूतपणे क्लस्टर केला आहे, ज्यामध्ये कमी परिवर्तनीयता किंवा सातत्य दर्शविले जाते.
• हाय स्टँडर्ड डेव्हिएशन: मोठे स्टँडर्ड डेव्हिएशन म्हणजे डाटा पॉईंट्स विस्तृत श्रेणीच्या मूल्यात पसरले जातात. हे डाटासेटमध्ये उच्च परिवर्तनीयता आणि अधिक अनिश्चितता दर्शविते.

उदाहरणार्थ, जर तुमच्याकडे समान अर्थासह दोन डाटासेट असतील:

• डाटासेट 1: [10,11,9,10,10]
• डाटासेट 2: [1,20,5,16,9]

जरी दोघांचेही अर्थ (10) असला तरी, डाटासेट 1 मध्ये खूपच कमी परिवर्तनीयता आहे, त्यामुळे त्याचे स्टँडर्ड डेव्हिएशन डाटासेट 2 पेक्षा कमी असेल.

4. स्टँडर्ड डेव्हिएशनचे वापर:

• फायनान्स आणि इन्व्हेस्टमेंट: स्टॉक किंवा पोर्टफोलिओसारख्या ॲसेटची अस्थिरता किंवा रिस्क मोजण्यासाठी स्टँडर्ड डेव्हिएशनचा वापर केला जातो. उच्च स्टँडर्ड डेव्हिएशन अधिक किंमतीतील चढ-उतार दर्शविते, ज्यामुळे अधिक रिस्क सूचित होऊ शकते.
• गुणवत्ता नियंत्रण: उत्पादनात, स्टँडर्ड डेव्हिएशन उत्पादनाच्या सातत्यचे मूल्यांकन करण्यास मदत करते. उत्पादन मोजमापातील लहान मानक विचलन हे दर्शविते की उत्पादने उच्च अचूकतेसह तयार केले जात आहेत.
• अंक ज्योतिष: डाटाचा प्रसार समजून घेण्यासाठी आणि आत्मविश्वास अंतर, रिग्रेशन मॉडेल्स आणि हायपोथेसिस टेस्ट यासारख्या इतर सांख्यिकीय उपाय कॅल्क्युलेट करण्यासाठी स्टँडर्ड डेव्हिएशनचा वापर केला जातो.

5. सामान्य वितरणाशी संबंध:

सामान्य वितरणात (बेल-आकारचे वक्र), विषयी:

• डाटाच्या 68% अर्थाच्या 1 स्टँडर्ड डेव्हिएशनमध्ये येते,
• 95% 2 स्टँडर्ड डेव्हिएशनमध्ये येते आणि
• 99.7% 3 स्टँडर्ड डेव्हिएशनमध्ये येते.

याला 68-95-99.7 नियम किंवा सामंजस्यपूर्ण नियम म्हणून ओळखले जाते, जे डाटाचे वितरण समजून घेण्यात स्टँडर्ड डेव्हिएशन कशी महत्त्वाची भूमिका बजावते हे दर्शविते.

6. उदाहरण:

खालील डाटासेटचा विचार करा: [4,8,6,5,3]

स्टेप 1: अर्थ कॅल्क्युलेट करा ( ⁇ ):

μ=4+8+6+5+3/5=5.2

स्टेप 2: प्रत्येक डाटा पॉईंटचा अर्थ सबट्रॅक्ट करा आणि परिणाम स्क्वेअर करा:

(4 - 5.2) ² = 1.44 ,

(8 - 5.2) ² = 7.84 ,

(6 - 5.2) ² = 0.64 ,

(5 - 5.2) ² = 0.04 ,

(3 - 5.2) ² = 4.84

स्टेप 3: सरासरी चुकता फरक (नमुना स्टँडर्ड डेव्हिएशनसाठी, एन--1=4 द्वारे विभाजित करा):

1.44+7.84+0.64+0.04+4.84/4=3.20

स्टेप 4: 3.20 चा स्क्वेअर रूट घ्या:

s=√3.20≈1.79

त्यामुळे, डाटासेटचे स्टँडर्ड डेव्हिएशन अंदाजित 1.79 आहे.

निष्कर्ष:

स्टँडर्ड डेव्हिएशन हे एक शक्तिशाली सांख्यिकीय साधन आहे जे डाटासेटमध्ये परिवर्तनीयतेची रक्कम मोजण्यास मदत करते. जोखीम मूल्यांकन करण्यासाठी, सातत्य मोजण्यासाठी आणि डाटा वितरण समजून घेण्यासाठी हे विस्तृत श्रेणीच्या ॲप्लिकेशन्समध्ये वापरले जाते. मोठ्या डाटासेटची गणना करणे थोडे अधिक जटिल असू शकते, परंतु हे डाटाच्या प्रसार विषयी मौल्यवान अंतर्दृष्टी प्रदान करते आणि वित्त, अभियांत्रिकी आणि संशोधन यासारख्या क्षेत्रांमध्ये व्यापकपणे वापरले जाते.