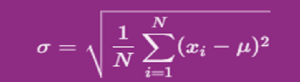मानक विचलन

मानक विचलन एक सांख्यिकीय माप है जो डेटा मानों के सेट में परिवर्तन या विक्षेप की मात्रा को निर्धारित करता है. यह दिखाता है कि डेटासेट के अर्थ (औसत) से कितना व्यक्तिगत डेटा पॉइंट अलग होते हैं. लो स्टैंडर्ड डेविएशन दर्शाता है कि डेटा पॉइंट अर्थ के करीब हैं, जबकि हाई स्टैंडर्ड डेविएशन से पता चलता है कि डेटा एक विस्तृत रेंज में फैला हुआ है. स्टैंडर्ड डेविएशन का इस्तेमाल आमतौर पर अस्थिरता का आकलन करने, जोखिम का अनुमान लगाने और डेटा डिस्ट्रीब्यूशन को समझने के लिए फाइनेंस, साइंस और इंजीनियरिंग जैसे क्षेत्रों में किया जाता है. यह वेरिएंस का वर्गमूल है, जो स्प्रेड के अधिक व्याख्यात्मक माप प्रदान करता है.

स्टैंडर्ड डेविएशन (एसडी) आंकड़ों में एक मूलभूत अवधारणा है जो डेटासेट के अर्थ (औसत) के चारों ओर डेटा प्वॉइंट के सेट के विघटन या प्रसार को मापता है. यह हमें यह महसूस करता है कि डेटा में वेरिएबिलिटी को समझने में मदद करने में औसतन, व्यक्तिगत डेटा पॉइंट का मतलब है कि कितना दूर है.

1. मानक विचलन के लिए फॉर्मूला:

आबादी (यानी, पूरे डेटासेट) के लिए, निम्नलिखित फॉर्मूला का उपयोग करके स्टैंडर्ड डेविएशन की गणना की जाती है:

कहां:

• ⁇ जनसंख्या मानक विचलन है.
• N जनसंख्या में डेटा बिंदुओं की संख्या है.
• xi प्रत्येक डेटा पॉइंट को दर्शाता है.
• ⁇ जनसंख्या का मतलब है (औसत).
• ⁇ सभी डेटा पॉइंट पर राशि दर्शाता है.

सैंपल के लिए (यानी, आबादी का एक सबसेट), फॉर्मूला थोड़ा छोटा आकार के हिसाब से समायोजित किया जाता है और कम वेरिएबिलिटी से बचता है:

s=

कहां:

• s एक सैंपल स्टैंडर्ड डेविएशन है.
• n सैम्पल में डेटा पॉइंट की संख्या है.
• X ⁇ सैम्पल का मतलब है.

2. मानक विचलन की गणना करने के चरण:

1. मियन की गणना करें: डेटासेट का औसत खोजें. यह सभी डेटा पॉइंट को समाइन करके और डेटा पॉइंट की कुल संख्या से विभाजित करके किया जाता है.

⁇ = ⁇ i^एन = 1 ^xi/एन

मान से अंतर खोजें: यह निर्धारित करने के लिए प्रत्येक डेटा पॉइंट से मतलब को सबट्रैक्ट करें कि प्रत्येक वैल्यू कैसे मतलब से विचलित होती है.

1. विभिन्नताएं वर्ग करें: चरण 2 में प्राप्त प्रत्येक अंतर वर्ग. यह चरण यह सुनिश्चित करता है कि नकारात्मक और सकारात्मक विचलन एक-दूसरे को रद्द न करें.
2. स्कॉयर्ड अंतर औसत: आबादी के लिए, एनएनएन (डेटा पॉइंट की संख्या) द्वारा विभाजित करके इन स्क्वेयर अंतरों का औसत देखें. सैंपल के लिए, एन--1 से सैम्पल साइज़ को अकाउंट में विभाजित करें और पूर्वग्रह को कम करें.
3. स्क्वेयर रूट लें: अंत में, चरण 4 से परिणाम का स्क्वेयर रूट लें . यह स्टैंडर्ड डेविएशन देता है.

3. मानक विचलन का इंटरप्रेशन:

• कम स्टैंडर्ड डेविएशन: एक छोटे स्टैंडर्ड डेविएशन का मतलब है कि डेटा पॉइंट का मतलब है. डेटा टाइट से क्लस्टर किया गया है, जो कम वेरिएबिलिटी या निरंतरता को दर्शाता है.
• हाई स्टैंडर्ड डेविएशन: एक बड़े स्टैंडर्ड डेविएशन का मतलब है कि डेटा पॉइंट विभिन्न प्रकार के मूल्यों में फैले जाते हैं. यह डेटासेट में उच्च वेरिएबिलिटी और अधिक अनिश्चितता को दर्शाता है.

उदाहरण के लिए, अगर आपके पास एक ही अर्थ के साथ दो डेटासेट हैं:

• डेटासेट 1: [10,11,9,10,10]
• डेटासेट 2: [1,20,5,16,9]

हालांकि दोनों का एक ही अर्थ है (10), लेकिन डेटासेट 1 में बहुत कम वेरिएबिलिटी होती है, इसलिए इसका स्टैंडर्ड डेविएशन डेटासेट 2 से कम होगा.

4. मानक विचलन का उपयोग:

• फाइनेंस और इन्वेस्टमेंट: स्टैंडर्ड डेविएशन का उपयोग स्टॉक या पोर्टफोलियो जैसी एसेट की अस्थिरता या जोखिम को मापने के लिए किया जाता है. उच्च मानक विचलन कीमतों में अधिक उतार-चढ़ाव को दर्शाता है, जो अधिक जोखिम को दर्शा सकता है.
• गुणवत्ता नियंत्रण: निर्माण में, स्टैंडर्ड डेविएशन प्रोडक्ट की स्थिरता का आकलन करने में मदद करता है. उत्पादन मापन में एक छोटा मानक विचलन दर्शाता है कि उत्पाद उच्च सटीकता के साथ उत्पादित किए जा रहे हैं.
• अंकिअंश: मानक विचलन का उपयोग डेटा के प्रसार को समझने और कॉन्फिडेंस इंटरवल, रिग्रेशन मॉडल और हाइपोथेसिस टेस्ट जैसे अन्य सांख्यिकीय उपायों की गणना करने के लिए किया जाता है.

5. सामान्य वितरण से संबंध:

सामान्य वितरण में (बेल आकार के वक्र), के बारे में:

• डेटा का 68% अर्थ के 1 स्टैंडर्ड डेविएशन के भीतर आता है,
• 95% 2 स्टैंडर्ड विचलन के भीतर आता है, और
• 99.7% 3 स्टैंडर्ड डेविएशन के भीतर आता है.

इसे 68-95-99.7 नियम या सहानुभूतिपूर्ण नियम के रूप में जाना जाता है, जो यह दर्शाता है कि डेटा के वितरण को समझने में स्टैंडर्ड डेविएशन कैसे महत्वपूर्ण भूमिका निभाता है.

6. उदाहरण:

निम्नलिखित डेटासेट पर विचार करें: [4,8,6,5,3]

चरण 1: मतलब की गणना करें ( ⁇ ):

μ=4+8+6+5+3/5=5.2

चरण 2: प्रत्येक डेटा पॉइंट से मतलब को घटाएं और परिणाम स्क्वेयर करें:

(4 - 5.2) ² = 1.44 ,

(8 - 5.2) ² = 7.84 ,

(6 - 5.2) ² = 0.64 ,

(5 - 5.2) ² = 0.04 ,

(3 - 5.2) ² = 4.84

चरण 3: स्क्वेयर के अंतर औसत (सैम्पल स्टैंडर्ड डेविएशन के लिए, N-1 = 4 से विभाजित करें):

1.44+7.84+0.64+0.04+4.84/4=3.20

चरण 4: 3.20 का वर्गमूल लें:

s=√3.20≈1.79

इस प्रकार, डेटासेट का मानक विचलन लगभग 1.79 है.

निष्कर्ष:

स्टैंडर्ड डेविएशन एक शक्तिशाली सांख्यिकीय टूल है जो डेटासेट में वेरिएबिलिटी की मात्रा को मापने में मदद करता है. इसका इस्तेमाल जोखिम का आकलन करने, निरंतरता को मापने और डेटा डिस्ट्रीब्यूशन को समझने के लिए एप्लीकेशन की विस्तृत रेंज में किया जाता है. हालांकि बड़े डेटासेट की गणना करना थोड़ा अधिक जटिल हो सकता है, लेकिन यह डेटा के प्रसार के बारे में मूल्यवान जानकारी प्रदान करता है और इसे फाइनेंस, इंजीनियरिंग और रिसर्च जैसे क्षेत्रों में व्यापक रूप से इस्तेमाल किया जाता है.