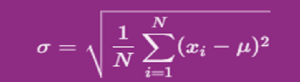સ્ટાન્ડર્ડ ડેવિએશન એક આંકડાકીય માપ છે જે ડેટા મૂલ્યોના સેટમાં વેરિએશન અથવા ડિસ્પર્શનની રકમને ક્વૉન્ટિફાઇ કરે છે. તે દર્શાવે છે કે ડેટાસેટના મીન (સરેરાશ) થી કેટલા વ્યક્તિગત ડેટા પૉઇન્ટ અલગ છે. ઓછા સ્ટાન્ડર્ડ ડેવિએશન સૂચવે છે કે ડેટા પૉઇન્ટનો અર્થ એ છે કે નજીક છે, જ્યારે ઉચ્ચ સ્ટાન્ડર્ડ ડેવિએશન સૂચવે છે કે ડેટા વ્યાપક શ્રેણીમાં ફેલાયેલ છે. સ્ટાન્ડર્ડ ડેવિએશનનો ઉપયોગ સામાન્ય રીતે અસ્થિરતાનું મૂલ્યાંકન કરવા, જોખમની આગાહી કરવા અને ડેટા વિતરણને સમજવા માટે ફાઇનાન્સ, સાયન્સ અને એન્જિનિયરિંગ જેવા ક્ષેત્રોમાં કરવામાં આવે છે. તે વેરિયન્સનો સ્ક્વેર રૂટ છે, જે સ્પ્રેડનું વધુ અર્થઘટનીય માપ પ્રદાન કરે છે.
સ્ટાન્ડર્ડ ડેવિએશન (એસડી) આંકડાઓમાં એક મૂળભૂત ખ્યાલ છે જે ડેટાસેટના અર્થ (સરેરાશ) ની આસપાસ ડેટા પોઇન્ટના સેટના વિતરણ અથવા પ્રસારને માપે છે. તે અમને એ સમજણ આપે છે કે, સરેરાશ, વ્યક્તિગત ડેટા પૉઇન્ટનો અર્થ કેટલો છે, જે ડેટામાં વેરિએબિલિટીને સમજવામાં મદદ કરે છે.
- સ્ટાન્ડર્ડ ડેવિએશન માટે ફોર્મ્યુલા:
વસ્તી (એટલે કે, સંપૂર્ણ ડેટાસેટ) માટે, નીચેના ફોર્મ્યુલાનો ઉપયોગ કરીને સ્ટાન્ડર્ડ ડેવિએશનની ગણતરી કરવામાં આવે છે:
જ્યાં:
- SN એ વસ્તી સ્ટાન્ડર્ડ ડેવિએશન છે.
- n એ વસ્તીમાં ડેટા પૉઇન્ટની સંખ્યા છે.
- xi દરેક ડેટા પૉઇન્ટને રજૂ કરે છે.
- μ વસ્તીનો અર્થ છે (સરેરાશ).
- n તમામ ડેટા પૉઇન્ટ પર સમ નોંધ કરે છે.
નમૂના માટે (એટલે કે, વસ્તીનો પેટા સમૂહ), ફોર્મ્યુલા નાના કદ માટે ધ્યાનમાં લેવા માટે સહેજ એડજસ્ટ કરવામાં આવે છે અને ઓછા અંદાજિત વેરિએબિલિટીને ટાળવામાં આવે છે:
એસ=
જ્યાં:
- s એ સેમ્પલ સ્ટાન્ડર્ડ ડેવિએશન છે.
- n એ સેમ્પલમાં ડેટા પૉઇન્ટની સંખ્યા છે.
- x નમૂનાનો અર્થ છે.
- સ્ટાન્ડર્ડ ડેવિએશનની ગણતરી કરવાના પગલાં:
- ગણતરીનો અર્થ: ડેટાસેટની સરેરાશ શોધો. આ તમામ ડેટા પૉઇન્ટને સમ કરીને અને કુલ ડેટા પૉઇન્ટ દ્વારા વિભાજિત કરીને કરવામાં આવે છે.
μ = iN=1xi/N
માધ્યમથી તફાવતો શોધો: દરેક મૂલ્યનો અર્થ કેટલો થાય છે તે નક્કી કરવા માટે દરેક ડેટા પૉઇન્ટમાંથી ઘટાડો.
- ચોરસ તફાવતો: પગલું 2 માં મેળવેલ દરેક તફાવતોને ચોરસ કરો. આ પગલું સુનિશ્ચિત કરે છે કે નકારાત્મક અને સકારાત્મક વિચલન એકબીજાને રદ કરતા નથી.
- સરેરાશ સ્ક્વેર્ડ તફાવતો: વસ્તી માટે, એનએનએન (ડેટા પૉઇન્ટની સંખ્યા) દ્વારા વિભાજિત કરીને આ સ્ક્વેર્ડ તફાવતોની સરેરાશ શોધો. નમૂના માટે, નમૂના સાઇઝ અને પૂર્વગ્રહ ઘટાડવા માટે n − 1 દ્વારા વિભાજિત કરો.
- સ્ક્વેર રૂટ લો: આખરે, પગલું 4 થી પરિણામનો સ્ક્વેર રૂટ લો. આ સ્ટાન્ડર્ડ ડેવિએશન આપે છે.
- સ્ટાન્ડર્ડ ડેવિએશનનું અર્થઘટન:
- ઓછા સ્ટાન્ડર્ડ ડેવિએશન: નાના સ્ટાન્ડર્ડ ડેવિએશનનો અર્થ એ છે કે ડેટા પૉઇન્ટનો અર્થ એ છે કે તેની નજીક છે. ડેટાને ટાઇટલી ક્લસ્ટર કરવામાં આવે છે, જે ઓછી વેરિએબિલિટી અથવા સાતત્યને દર્શાવે છે.
- ઉચ્ચ માનક વિચલન: મોટા પ્રમાણભૂત વિચલનનો અર્થ એ છે કે ડેટા પૉઇન્ટ વિશાળ શ્રેણીના મૂલ્યો પર ફેલાયેલ છે. આ ડેટાસેટમાં ઉચ્ચ વેરિએબિલિટી અને વધુ અનિશ્ચિતતાને સૂચવે છે.
ઉદાહરણ તરીકે, જો તમારી પાસે સમાન અર્થ સાથે બે ડેટાસેટ હોય:
- ડેટાસેટ 1: [10, 11, 9, 10, 10]
- ડેટાસેટ 2: [1, 20, 5, 16, 9]
જોકે બંનેનો અર્થ સમાન છે (10), ડેટાસેટ 1 માં ખૂબ ઓછી વેરિએબિલિટી છે, તેથી તેનું સ્ટાન્ડર્ડ ડેવિએશન ડેટાસેટ 2 કરતાં ઓછું હશે.
- સ્ટાન્ડર્ડ ડેવિએશનના ઉપયોગો:
- ફાઇનાન્સ અને ઇન્વેસ્ટમેન્ટ: સ્ટૉક અથવા પોર્ટફોલિયો જેવા એસેટની અસ્થિરતા અથવા જોખમને માપવા માટે સ્ટાન્ડર્ડ ડેવિએશનનો ઉપયોગ કરવામાં આવે છે. ઉચ્ચ સ્ટાન્ડર્ડ ડેવિએશન કિંમતના વધઘટને સૂચવે છે, જે વધુ જોખમને સૂચવી શકે છે.
- ગુણવત્તા નિયંત્રણ: ઉત્પાદનમાં, સ્ટાન્ડર્ડ ડેવિએશન ઉત્પાદનની સ્થિરતાનું મૂલ્યાંકન કરવામાં મદદ કરે છે. ઉત્પાદનના માપમાં નાના પ્રમાણભૂત વિચલન સૂચવે છે કે ઉત્પાદનો ઉચ્ચ ચોકસાઈ સાથે ઉત્પાદિત કરવામાં આવી રહ્યા છે.
- આંકડાઓ: ડેટાના પ્રસારને સમજવા અને આત્મવિશ્વાસના અંતરાલ, રિગ્રેશન મોડેલ અને હાઇપોથેસિસ ટેસ્ટ જેવા અન્ય આંકડાકીય પગલાંઓની ગણતરી કરવા માટે સ્ટાન્ડર્ડ ડેવિએશનનો ઉપયોગ કરવામાં આવે છે.
- સામાન્ય વિતરણ સાથે સંબંધ:
સામાન્ય વિતરણમાં (બેલ-આકારના વક્ર), આ વિશે:
- 68% ડેટા 1 સ્ટાન્ડર્ડ ડેવિએશન ઑફ મીનની અંદર આવે છે,
- 95%. 2 સ્ટાન્ડર્ડ ડેવિએશનની અંદર આવે છે, અને
- 99.7% falls within 3 standard deviations.
This is known as the 68-95-99.7 rule or the empirical rule, which highlights how standard deviation plays a key role in understanding the distribution of data.
- ઉદાહરણ:
Consider the following dataset: [4, 8, 6, 5, 3]
Step 1: Calculate the mean (μ):
μ=4+8+6+5+3/5=5.2
Step 2: Subtract the mean from each data point and square the result:
(4−5.2)2=1.44,
(8−5.2)2=7.84,
(6−5.2)2=0.64,
(5−5.2)2=0.04,
(3−5.2)2=4.84
Step 3: Average the squared differences (for sample standard deviation, divide by n−1=4):
1.44+7.84+0.64+0.04+4.84/4=3.20
Step 4: Take the square root of 3.20:
s=√3.20≈1.79
Thus, the standard deviation of the dataset is approximately 1.79.
નિષ્કર્ષ:
Standard deviation is a powerful statistical tool that helps quantify the amount of variability in a dataset. It is used in a wide range of applications to assess risk, measure consistency, and understand data distribution. મોટા ડેટાસેટની ગણતરી કરવા માટે તે થોડી વધુ જટિલ હોઈ શકે છે, પરંતુ તે ડેટાના પ્રસાર વિશે મૂલ્યવાન સમજ પ્રદાન કરે છે અને ફાઇનાન્સ, એન્જિનિયરિંગ અને સંશોધન જેવા ક્ષેત્રોમાં વ્યાપકપણે ઉપયોગમાં લેવાય છે.
