- Study
- Slides
- Videos
3.1 Option Pricing

The value of any given option is composed of two components:
- Intrinsic value
- Extrinsic value
Option Price= Intrinsic Value + Extrinsic Value
Intrinsic Value
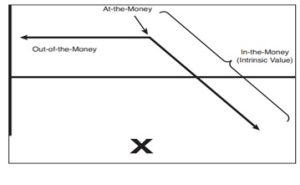
The intrinsic value of an option is the amount that the market price is higher than the strike price for a call and lower than the strike for a put. In other words, the intrinsic value is the amount of money that the option would be worth if it expired today. For the option to have intrinsic value, the option must be in-the-money.
In-the-money and out-of-the-money are often falsely used by beginning traders. Many traders refer to a profitable option trade as being in-the-money. However, this is not the case. An option can be in-the-money and not profitable. Likewise it can be out-of-the-money and be a profitable trade.
Call options are described in the following way:
- In-the-money – The futures price is above the strike price.
- At-the-money – The futures price is at the strike price.
- Out-of-the-money – The futures price is below the strike price
The intrinsic value of a call option
Put options are described in the following way:
- In-the-money – The futures price is below the strike price.
- At-the-money – The futures price equals the strike price.
- Out-of-the-money – The futures price is above the strike price.
The intrinsic value of a put option
As shown below, the intrinsic value increases tick for tick as the market moves beyond the strike price of the option. For example, if you own a Dabur stock call option of a strike price of Rs.370. With the market at 380 the option has an intrinsic value of Rs.10; if the market price moves to Rs.390 the option has an intrinsic value of Rs.20 and so on. It is important to realize that before expiration the option value will never be equal to the intrinsic value because it will also have extrinsic, or time, value.
Extrinsic Value
Extrinsic value is based on a combination of the strike price, time, volatility, and demand. Extrinsic value is like the “icing on the cake.” Due to the nature of its components, it is impossible to estimate extrinsic value. Beginning traders often ask questions such as, “If I buy a call and the market goes up x number of points, what will it be worth?” Unfortunately, the answer depends on factors that can’t necessarily be measured quantitatively.
Example– If a trader buys a September Rs.6000 soybean call option for Rs.100 in June with the underlying futures price at 5800 and the market rallies to Rs6000 by the beginning of July, the option will likely be worth much more than the original premium paid. After all, there will still be a lot of time value left on the option and the option is now at-the money.
If a trader buys the same option, in the same circumstances, but it takes the underlying futures until August to reach Rs.6000, the trade will likely be a loser. More time premium would have eroded from the option value than it would have benefitted from the market being closer to the strike price.
As you can see, it is possible to be right in the direction of the market and still lose money on a long option trade. This is exactly why it is so difficult to make money as an option buyer. It is hard enough to be right, but direction is only the first obstacle. The extrinsic value of an option is based on a combination of the following factors:
- Time
- Volatility
- Demand
Of these factors, time is the only predictable element. You know what they say, “Time waits for no man.”
It is important to realize that all calculations are based on the assumption that the trade is held until expiration. This is because at expiration the options will have no extrinsic value, which is nearly impossible to predict at any given point. At any time prior to expiration, the profit or loss experienced on the trade may be outside the original profit and loss parameters based on the price of the underlying contract at option expiration. This is especially true in the case of option spreads.
Time Value
The longer the amount of time until an option’s expiration, the greater the time value of a particular option will be. This makes sense, because the longer the buyer possesses the right to exercise the option the more valuable that right is. Remember, in commodity trading anything can happen. It is not out of the question for a relatively worthless option to come to life and post abnormal gains (or losses for the seller) by expiration. Keep in mind that this is the exception rather than the rule, but it can and does happen.
Volatility
If the price of the underlying futures contract is fluctuating considerably, there is both a greater profit and a greater loss potential. Thus options tend to be more expensive to buy when volatility is high. Likewise, sellers will collect more premium for a short option during times of inflated volatility. Of course, premiums are high for a reason – the risk and reward are equally magnified.
Trading Volatility
Because of the effect volatility has on option premium, it is a good idea to buy options when the market is quiet and sell them in times of high volatility. Those holding long options during an explosion in volatility have been known to enjoy impressive profits. On the other hand, short option traders may find themselves in a less than desirable position should they be in a market that experiences significant increases in volatility after they have entered a position.
Demand
If the number of traders willing to buy an option at a given price is greater than the number of traders willing to sell the same option, the value of that option appreciates. It is the nature of the option markets to experience high demand of call options in a market that is in an uptrend and high demand of put options in a downtrend. Thus, it is not uncommon to see overpriced options in such scenarios. An interesting phenomenon in the equity indices, put options are almost always priced high to comparative calls. This is partly due to equity holders hedging their portfolios along with the expectation that markets drop faster than they go up. You may have heard the concept of higher put valuation referred to in the context of a “volatility smile” or “skewed volatility.”
In the case of equity indices the implied volatility of an at the-money option is often less than that of an out-of-the-money option, or negatively skewed. This is especially true in the case of distant strike priced puts; interestingly, this didn’t seem to be the case until after the crash of 1987.
If you are unfamiliar with the term implied volatility, it is important to note that the term differs greatly from market volatility (often referred to as historical volatility). Historical or market volatility is a direct measure of price movement, while implied volatility is a function of the derivative value (option premium) itself rather than the underlier. Therefore, options with differing strike prices or expiration dates but based on the same underlier may have differing levels of implied volatility. The formal definition of implied volatility is, in its simplest form, the volatility implied by the market price of the option
Another component of demand is strike price. Strike price is obviously one of the biggest factors in the market’s determination of option value. The closer to the money an option is, the more valuable it is to the buyer and the riskier it is to the seller. This makes sense; people are willing to pay more for an option that seems to have a better chance of paying out than they would for an option that will most likely expire worthless. The delta value of an at-the-money option is 50 and has roughly 50 percent odds of expiring in-the-money.
3.2 Properties of Option Values

1. The minimum value of an option is zero-
This is because an option is only a choice, not an obligation. The value of an option cannot be negative, because you do not have to do anything to get rid of it. The option will always have a zero, or a positive value.
2. The maximum value of a call option is equal to the value of the underlying asset.
This makes a lot of economic sense. An option allows you to buy a given asset at a certain exercise price. The most valuable option will be the one that allows you to acquire the asset at no cost, and the value of this option will be equal to the value of the underlying asset.
3. The total value of an option is the sum of its intrinsic value and its time premium
Total value= Intrinsic Value of the option+ Time Premium of the option
The intrinsic value of an option is the value, or benefit, obtained by the holder by exercising the option immediately. The time premium of the option is its value, or benefit, of being able to wait and see. At expiration, the ability to wait is not there and so the time value of the option becomes zero.
The intrinsic value of a call option equals the difference between the stock price and the exercise price, if the stock price is higher; or the intrinsic value is zero- the stock price is less than the exercise price.
Intrinsic value of a call = max [Stock Price – Exercise Price, 0]
The value of a put option increases as the stock price drops. This enables us to write
Intrinsic value of a put = max [Exercise Price – Stock Price, 0]
An option has time value only before its expiration. You lose the time value of an option when you exercise it before its expiration. Therefore, generally, it is not desirable to exercise an option before maturity. There is an important exception to this rule when we are evaluating the call options on dividend-paying stocks. When a stock pays cash dividends its price drops on the ex-dividend date, and the value of the call drops proportionately. If the time value of the option is less than the present value of the dividends paid during the life of the option, then it is better to forgo the time value of the option and capture the present value of the dividends.
For example, when a stock is selling for Rs.60 a share, its call option with exercise price Rs.55 is selling for Rs.8. Then the intrinsic value of the call is R.5 and the time value Rs.3.
For another option priced at Rs.3 with stock price Rs.79 and exercise price Rs.80, the intrinsic value is zero, and hence the time premium is Rs.3
4. At expiration, the value of a call option is zero if one cannot derive any economic benefit out of it. This is the case when the final stock price is less than the exercise price. One could buy the stock directly at a cheaper price and not use the call option. If we are not going to use an option, its value is zero.
On the other hand, if the stock price is greater than the exercise price, then it is desirable to use the option and get the stock at a lower price, equal to the exercise price. The net advantage of using the option is just the difference between the final stock price and the exercise price.
5. In general, the value of an American option is higher than that of a European option.
One may exercise an American option at any time before expiration, but one can exercise a European option at its expiration only. This means that an American option offers greater flexibility to the option holder. A European is more restrictive, because you can utilize it only at its expiration. Thus, an American option is more desirable.
6.The maximum value of an American put is equal to its exercise price. We may exercise an American put at any time before expiration, allowing us to sell the stock at the exercise price. Therefore, the maximum amount that a put can realize is the exercise price.
7. A call with a higher exercise price has lower value compared to a similar call with lower exercise price. At expiration, the calls are in the money, if the stock price is higher than the exercise price. They are out of the money when the stock price ends up being less than the exercise price. For the call option to be of any value, the stock price must cross over the exercise price hurdle. Before maturity, the higher the exercise price, the lesser is the probability of jumping over it. Thus, the higher exercise price option is less valuable.