What Are Option Greeks In Stock Market

7.1 Introduction

For an option trader to be successful in the market there are several forces which need to work in his favour. These forces are collectively called ‘The Option Greeks’. These forces influence an option contract in real time, affecting the premium to either increase or decrease. These forces not only influence the premiums directly but also influence each another.
Options Premiums, options Greeks, and the natural demand supply situation of the markets influence each other. Though all these factors work as independent agents, yet they are all intervened with one another. The final outcome of this mixture can be assessed in the option’s premium. For an options trader, assessing the variation in premium is most important. He needs to develop a sense for how these factors play out before setting up an option trade.
Thus, option Greeks generally measure the sensitivity of the option price to various parameters that impact the value of an option. Such sensitivity can either be on the positive side or on the negative side.
The Greeks include variables represented by the Greek letters Delta, Gamma, Theta, Vega, and Rho.
1. Delta – Measures the rate of change of options premium based on the directional movement of the underlying
2. Gamma – Rate of change of delta itself
3. Vega – Rate of change of premium based on change in volatility
4. Theta – Measures the impact on premium based on time left for expiry
5. Rho – Measures the sensitivity of the interest rate on the value

7.2 Delta

Delta (Δ) represents the sensitivity of an option’s price to changes in the value of the underlying security. In other words, how much does the price of the option go up or down as the price of the security goes up and down?

Delta measures how much the price of the option will change as a result of a Rs.1 change in the price of the asset. The Delta of an option varies over the life of that option, depending on the underlying stock price and the amount of time left until expiration.

Example:

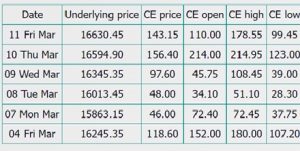
See the two snapshots below: It belongs to Nifty’s 16800 CE option.

Look at the change in premium – on 4th March when Nifty was at 16245 the call option was trading at 118, however on 11th March when Nifty moved to 16630 and the same call option was trading at 143
On 7th March – when Nifty declined to 15863 and so did the option premium declined to 46.
From the above table – as and when the value of the spot changes, so does the option premium. More precisely as we already know – the call option premium increases with the increase in the spot value and vice versa.
From the snapshots above you that premium will certainly change with change in value of the underlying – but by how much? What is the likely value of the 16800 CE premium if Nifty reaches 16600?
Well, this is exactly where the ‘Delta of an Option’ comes handy. The Delta measures how an options value changes with respect to the change in the underlying. In simpler terms, the Delta of an option helps us answer questions of this sort – “By how many points will the option premium change for every 1 point change in the underlying?”
Therefore the Option Greek’s ‘Delta’ captures the effect of the directional movement of the market on the Option’s premium.
For example- A trader may choose to hold the option in lieu of purchasing the stock. Say you buy 1 call to control 100 shares of ITC. If ITC rises by Rs.1 you would expect to gain on the option, but how much?
To answer this question you must consider the delta of your option. Delta is stated as a percentage. If your ITC option has a delta of 50, that means that according to the model the option premium should change 50% in relation to the change in the price of the stock

Here’s how it works:

ITC Stock Price Rs200——- goes to—- Rs. 210 [Rs.10 gain]

Call Premium of  Rs.2 ==============.50 DELTA ============= Rs.2 + .5 = Rs.2.50

Deltas are always positive, because there is a positive correlation between the price of a stock and the option premium. The option premium price is directly related to the price of the stock [i.e., stock price goes up, option premium goes up, and vice versa].

On the other hand, a put option premium has a negative correlation to the underlying stock price. If the stock price goes up, then the value of the put should decline and vice versa. So, for example,

ITC Stock Price Rs.200——————–goes to———— Rs.210 (Rs.10 gain)

Put Premium  Rs.2————————-0.50 delta——- Rs2-0.50= 1.50

In reality the changes in option premium values is not linear and so you have to keep in mind that if ITC were to increase in value by Rs.1, the option price might change by more than what is indicated in these examples.

Additionally the delta option varies between 0 and 1, the closer the delta is to 1, the more the option price will move in tandem to the underlying stock price [typical of a deep in-the- money option ]. If a stock were to have a delta of 1, the option premium would trade in exact relationship to the stock price. A Rs.1 increase in the stock price would cause a Rs.1 increase in the option premium. For 1 lot that controls 200 shares, this would be a Rs.200 gain. If an option trader purchased a 1 call with a delta of .60, this would be equivalent to controlling .60 x 200 or 120 shares to stock in terms of the movement in the stock price [i.e., a Rs.1 increase in the stock price on a call = Rs.1 x .600 x 200 x shares = Rs.120 or alternatively, you effectively control 200 x .60 = 120 shares, 120 shares x Rs1 gain = 120]. The delta is the option’s equivalent of a position in the underlying shares of stock based on the strength of the correlation between the option premium and the underlying price of the stock.

A trader who buys 5 call contracts on ITC with a delta of .45 has a position that is effectively long, 5 x 100 shares x .45 = 225 shares. In the parlance of the options market, we would say this trader is long 225 Deltas. Conversely, the same idea applies to puts. Being long 10 .60-delta puts makes the trader short a total of: 100 x 10 x .60 or 600 Deltas

Another way of analyzing delta is to say that it’s a statistical approximation of the chance of an option expiring in-the-money. An option with a .80 delta would have a 80% likelihood of being in-the-money at expiration. Because of changing options market conditions, deltas do not remain constant over time. Deltas are calculated from dynamic inputs – stock price, time to expiration, volatility, current interest rate, and strike price. When any of these inputs change it will have an impact on delta.

Impact of Time on Delta

In athletic events such as basketball, European football [a.k.a. soccer], or American football as time winds down, the elements that impact the ending of the game take on ever greater importance in terms of outcome. The reason why some coaches get exorbitant salaries [notwithstanding the Iowa college coaches] may be due to their abilities to manage risk or take advantage of opportunities in the last seconds of a game. The same phenomenon holds true for an options trader holding a position that may be close to expiration.
The more time an option has to expire, the less certainty there is about whether the option will be ITM or OTM at expiration. The deltas of both the put and call options will reflect that uncertainty. The more time left in the option, the closer the deltas tend to hover around .50. A delta of .50 represents the greatest uncertainty — a 50 -50chance of ending ITM. At expiration, the delta of the option is theoretically at 1.00 or 0 depending on whether you have a ITM or OTM situation.

Effect of Volatility on Delta
Consider the following estimated delta of a 50-Strike call in terms of volatility for an option on a stock trading between 50 and 60 over the last six months. The call has 90 days to expiration.

At a 10% volatility [little fluctuation in the underlying stock] the option delta is 1.00 [deeply ITM]. At that same volatility with the stock priced at $42, the option delta is 0 [OTM]. As volatility rises from 10 to 45%, delta increases for an OTM call. [ e.g. at $42, delta goes from 0 to .3]. On the other hand, for ITM option, more volatility actually lowers delta [i.e., the option premium may not trade in tandem with the underlying stock price], for example when the stock price is deep in the money at $58/share, delta goes from 1 down to .79 when volatility moves from 10% to 45%.
There are two main ways of measuring volatility in the underlying stock: (1) historical volatility [based on past stock prices] and (2) implied volatility [a byproduct of the Black Scholes Pricing Model]
Why is volatility so important to option traders? Volatility is significant to an options trader or stock purchaser, because volatility measures the possible price changes of the asset in the future. Assets that have high volatility can be expected to have large price changes in the future. As a result, options that are based on assets with high volatility can be expected to have higher prices. For example, someone who is long a call would find more volatility attractive, whereas, the seller of the call would like to have low volatility. Implied volatility is the markets view of where volatility will be in the future. To determine an option’s implied volatility, the trader must use a pricing model.
Lets understand an illustration:

Historical Volatility tells us how volatile as asset has been in the past. Implied Volatility is the markets view on how volatile as asset will be in the future. We can tell how high/low implied volatility is by comparing the market price of an option to the options theoretical fair value. This is why we need to use an option pricing model – to determine the fair value of an option and hence know if the market price for the option is over/under valued.

When the market price of an option is higher than its theoretical value (based off past information) it is considered expensive and so to if the market price of the option is less than the theoretical price, it is considered cheap.

7.3 Gamma

As understood in the previous chapter- Delta represents the change in premium for the given change in the underlying price.

For example if the Nifty spot value is 16000, then we know the 16200 CE option is OTM, hence its delta could be a value between 0 and 0.5. Let us fix this to 0.2 for the sake of this discussion.

Assume Nifty spot jumps 300 points in a single day, this means the 16200 CE is no longer an OTM option, rather it becomes slightly ITM option and therefore by virtue of this jump in spot value, the delta of 16200 CE will no longer be 0.2, it would be somewhere between 0.5 and 1.0, let us assume 0.8.

With this change in underlying, one thing is very clear – the delta itself changes. Meaning delta is a variable, whose value changes based on the changes in the underlying and the premium!

The Gamma of an option measures this change in delta for the given change in the underlying. In other words Gamma of an option helps us answer this question – “For a given change in the underlying, what will be the corresponding change in the delta of the option?”

Thus, Gamma tells you how much the Delta should change based on a Rs.1 move in the underlying. Remember, Gamma is measured in Delta!!!

Gamma & Remaining Time to Expiry

• Suppose there is a basket ball game. Team A & Team B both are of equal strength. At the time when the game starts, the score is 0 and 0 & both team’s chance of winning the game is 50%. This is analogus to purchasing an at the money call option with a delta of 0.5
• During the game, there are times when Team A is in front by a few points and it has a higher probability of winning the game. This is equivalent to the price of the underlying stock goes up and so does the delta of the call option.
  How much should the delta go up? This is the same question as the one we will ask regarding how big a chance is it for Team A to win the game at this time when it is leading by a few points.
• It all depends on how much time remains in the game if both the team are still of (approx.) equal strength. If Team A is leading by 3 points at half time, its winning chance surely is higher than 50% but probably not by much, say 55%. However, if Team A is leading by 3 points with only 30 seconds left in the game, its chance of winning is probably very high, say 95%. Although the margin of the lead for Team A is the same, the chance of winning is different.
• It is same for the options- Assume that for an at the money option with three months to the expiration date, the delta is 0.5 and the gamma is 0.02. After one day, the price of the underlying changes by one point. At this time, the delta may change from 0.50 to 0.52- a relatively small change because there is plenty of time for the price of the underlying to go either way.
• However, if the time is now one day before the expiration date, and the price of the underlying changes from the at the money to one point in the money, the delta of the option may change from .50 to .95 because it surely looks good for the option to be in the money before it expires. Gamma estimates the rate of change.
• For options which are far in the money (or far out of the money), gamma probably does not matter much because the delta is already close to 1 (or close to zero for far out of the money options). Just like the basketball game, if one team is leading by 30 points at the half, its chance of winning is very high. Whether it gains a couple of points of looses a couple of points in the second half shall not affect the results very much.

7.4 Theta

Option prices can be divided into two parts: (1) intrinsic value and (2) time value
Intrinsic value is the market price of the stock less the strike price for the ITM option. Time value is what is left over in terms of the premium paid on the option. The loss in the value of an option due to the passage of time is called decay or price erosion.
Theta (θ) is the rate of change in an option’s price given a unit change in the time to expiration. Theta is expressed in points lost per day when all other conditions remain the same. Time runs in one direction, hence theta is always a positive number, however to remind traders it’s a loss in options value it is sometimes written as a negative number. A Theta of -0.5 indicates that the option premium will lose -0.5 points for every day that passes by. For example, if an option is trading at Rs.2.75/- with theta of -0.05 then it will trade at Rs.2.70/- the following day (provided other things are kept constant). A long option (option buyer) will always have a negative theta meaning all else equal, the option buyer will lose money on a day by day basis. A short option (option seller) will have a positive theta.

How is Theta used?

Long Options and Theta
A long option holder is negative Theta, which equates to buying time. Since time is always depleting, a long option holder needs to capture the time purchased prior to the option expiring and/or experience a movement in the underlying greater than the amount of Theta purchased. Meaning – holding an option to expiration is only profitable if the underlying moves greater than the Theta purchased. Otherwise, Theta can be captured by closing the option prior to expiration.
For Example, if Co. A is trading at Rs,100 and a Co. A Rs.100 Call is purchased at Rs.3, the premium is primarily time value as executing on the contract is not more favorable than the market. If Co. A remains at Rs. 100 at expiration, the call will expire worthless. The buyer of Co. A Rs.100 Call will lose all of the premium purchased since time is up.
If Co. A was at Rs.105.00 on expiration, the Co.A Rs.100 Call will now be worth at least Rs.5 as the contract is more favorable than the market (buy at the strike, Rs.100.00 and sell at the market, Rs.105). However, the purchaser of the Co. A Rs.100 Call will capture Rs.2 of profit in this scenario as time value has completely decayed. The loss in this scenario is limited to the premium paid and has unlimited reward potential.
Negative Theta typically means time is not of favor however, the risk is limited to potentially make a higher reward.

Short Options and Theta

• A short option seller is positive Theta, which equates to selling time. As time depletes, the cheaper the option will become and is working in the seller’s favor. The option seller can capture profit if the underlying is neutral or is bearish or is bullish
  For Example, if Co. B is trading at Rs.100 and a Co.B Rs.100 Call is sold at Rs.3.00, the premium is primarily time value as executing on the contract is not more favorable than the market. If Co.B remains at 100 at expiration, the call will expire worthless. The seller of the Co.B 100 Call will keep all of the premium sold since time is up.
• If Co.B was at 105 on expiration, the Co.B 100 Call will now be worth at least Rs.5 as the contract is more favorable than the market (buy at the strike, Rs.100 and sell at the market, Rs. 105). However, the seller of the Co.B 100.00 Call will incur a loss of Rs.2 in this scenario as time value has completely decayed. The loss in this scenario has unlimited potential and the reward is limited to the premium sold.
• Positive Theta typically means time is of favor however, the reward is limited with increased risk potential.
  Thus, to summarise- for those who hold long options, theta hurts their positions because it reduces the value of the option. Take a 90-strike call with a theoretical value of Rs.3.16 on a stock at Rs.92 a share. The 32-day 90 call has a theta of .05.
• If a trader owns this position,.03 would be lost going from 32 to 31 days and so this trader would be negative theta. However, in the case of put there is a similar effect of time. Say the trader has a 32-day 90 strike put with a theta of .04. A put holder would theoretically lose .04 a day, while the put writer would theoretically make .04.

The Impact Moneyness has on Theta

Theta is not constant, and the impact of time on options pricing may be more non-linear in nature. On variable that influence’s changes to theta is whether the option is ATM. An at-the-money [ATM] option may have higher time value than one that is ITM or OTM. Therefore, with more time premium to lose, an ATM will have a higher decay rate than one that is either ITM or OTM. So, as the stock price changes there may be a revision in theta to reflect changes in moneyness.

Volatility’s Impact on Theta

The greater volatility in the underlying stock price, the higher the value of the option which offers larger decay at a faster rate. Cateris paribus, the higher the volatility, the higher theta.

7.5 Vega

• The option’s vega is a measure of the impact of changes in the underlying volatility on the option price. Specifically, the vega of an option expresses the change in the price of the option for every 1% change in underlying volatility.
• Options tend to be more expensive when volatility is higher. Thus, whenever volatility goes up, the price of the option goes up and when volatility drops, the price of the option will also fall. Therefore, when calculating the new option price due to volatility changes, we add the vega when volatility goes up but subtract it when the volatility falls.
• An options trader looking at various call premium prices on same price stocks, say trading at 35 a share, with a strike of 35 [trading at-the-money] will find significant differences in pricing despite these options having the same expiration date. What factor explains these differences? The price difference can be explained by volatility, the way the option price may change due to the volatility tied up in the underlying stock.

Implied Volatility[IM] and VEGA IV is a percentage change in the stock price based on the way an option is priced in the market. An estimate of IV, along with the other five variables is inputted into the option pricing model to render a theoretical value of the option. The theoretical value of the option may then be compared to the market value to determine whether the option is under or overpriced and by how much. IV levels can and do change over time. When IV rises or falls, the option price moves up or down in direct relation to volatility. Vega is the rate of change of an option’s theoretical value in relation to changes in implied volatility.
If the IV rises or declines by 1%, then the theoretical value of the option will rise or fall by the option’s VEGA. For example. A call with a theoretical value 2.0 has a VEGA of .05 and IV rises by 1% from 17 to 18%, then the new theoretical value of the call will be 2 + .05 or 2.05. If iV declines 1%, then the theoretical value of the option would be 2 – .05 or 1.95.
A put with the same expiration month and same strike on the same underlying stock will have the same VEGA value as its corresponding call. So, raising or lowering the IV by 1% would increase or decrease the theoretical value of the put by the VEGA amount.
Impact of Moneyness on VEGA

The stock price’s relationship to the strike price is a major determinant of an option’s VEGA. Implied volatility affects only the time value portion of an option. Because ATM options have the greatest amount of time value, they have higher VEGAs. ITM or OTM options have lower VEGAs.

How IV May Influence VEGA
As long as an option remains ATM the VEGA will stay a constant amount. However, once the stock price moves and the option is either ITM or OTM the Vega will be altered. Lower IV tends to reduce ITM and OTM VEGAS, while higher IV may cause VEGAS to go up for ITM or OTM options.

The Impact Time Has on VEGA
As time moves forward there will be less time premium in an option that can be impacted by IV. Therefore, VEGA gets smaller as expiration draws near. The reduction of VEGA for an ATM option may occur in a nonlinear fashion the closer you get to expiration.

How is Vega used?- Long and Short Option’s Vega

Long options have a positive Vega and short options have a negative Vega. When buying an option, the purchaser wants the premium to increase and when selling an option, the seller wants the premium to decrease. Should implied volatility increase, there will be an increase in the option’s premium. Inversely, if there is a decrease in implied volatility, there will be a decrease in the option’s premium. This is why Vega is positive for long (purchased) positions and negative for short (sold) positions.
Vega changes when there are larger price swings (higher implied volatility) which can be equated to higher uncertainty. Lower implied volatility can be connected to lower uncertainty, which equates to less dramatic swings of the underlying security.
A long Vega portfolio means there is positive exposure to increases in implied volatility and a short Vega portfolio is indicative of volatility vulnerability. Remember, high volatility can result in drastic market swings. Volatility typically has a negative correlation to the market – meaning spiked volatility can be reflective of downward market velocity. Managing a portfolio’s Vega exposure can help understand volatility risk and the trader’s comfort level.
Measuring Volatility
Vega can be used to measure volatility exposure in multi-leg option strategies or an option’s portfolio.
For example:
Long 1 XYZ 60 Call with 60 Days to Expiration at +.50 Vega (Long Volatility)
Short 1 XYZ 60 Call with 30 Days to Expiration at -.30 Vega (Short Volatility)
Net Vega: + .20 Vega
This trade is long Vega and has positive volatility exposure.
Note- Vega and implied volatility can change without any movement in the underlying. Vega should not be confused with volatility. Volatility can be an implied or a historical figure – Vega measures an option position’s sensitivity to implied volatility.

RHO
Rho measures the change in an option’s value (all other inputs to the model remaining constant) for a given change in interest rates, typically either 0.01% p.a. or 1% p.a.
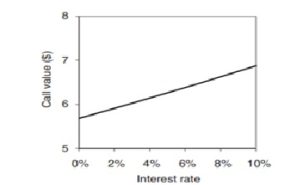
The graph below shows the value of a 100 strike ATM call as interest rates rise. It is a linear relationship and rho is the slope of the line in the graph. In this particular example rho is 0.12. This means that for a 1% increase in the interest rate the call option value (all other inputs remaining constant) increases by 12 paisa. Again this is on a per share basis and has to be increased in proportion to the number of shares in the option contract.

Rho on call options
The option pricing model assumes that when an option is written a riskless hedge can be put in place underlying shares to buy to cover the exposure. The model assumes, in effect, that this is funded through borrowing, offset by any dividend income received on the shares. All other things being equal, then, when interest rates rise the value of call options also tends to rise. The writers of calls pass on their higher funding costs to the buyers.
For Example:
Assume XYZ has a current market price of Rs.500

Buying Stock Value: Buy 100 Shares XYZ at 500 per Share = Rs. 50,000 Total Cost (500 x 100 Shares)

Buying Call Option: Buy 1 Rs500 Call at Rs.10
Premium = Rs.1,000 Total Cost (10 Premium X 1 Contract X 100 Shares)

The total exercisable value of this option is Rs.50,000 (right to buy 100 shares at Rs.500). The cost to purchase the option Rs.1,000 is less upfront capital than the total exercisable value, the remaining Rs.4,000 could be deposited and earn interest. This would be positively reflected in the value of the long call option as interest rates increase.

Rho on put options (Negative Rho)
On the other hand if interest rates rise the value of put options will tend to fall. Writers of put options are exposed to falls rather than rises in the price of the underlying share. To hedge this delta exposure they can run short positions in the underlying. As interest rates rise, they will earn more money by investing the cash received from selling the shares short, and can afford to pass the benefits on to the buyers of the puts.
For Example:

XYZ has a current market price of Rs.500
Shorting Stock Value: Sell 100 XYZ at Rs.500 per Share = Rs.5,000
Total Proceeds (50 x 100 Shares)
Buying Put Option: Buy 1 500 put at Rs.10
Premium = Rs.1,000 Total Cost (10 Premium X 1 Contract X 100 Shares)

The total exercisable value of this option is Rs.5,000.00 (right to sell 100 shares at 50.00). The cost to purchase the option (1,000) is more upfront capital than the proceeds the total exercisable value would generate. The Rs.5000 from the short sale could be deposited and earn interest. This would be negatively reflect in the value of the long put option as interest rates change.

7.6 SUMMARY OF GREEKS

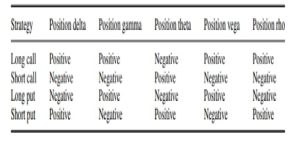
The table below summarizes the ‘signs’ of the Greeks for four basic option strategies: long or short a call; long or short a put. To take one example from Table below, a long call has positive delta (it profits from a rise in the share price). It has positive gamma or convexity, which means that the profits accelerate in a more than linear fashion as the price of the underlying rises.
As the underlying price falls the losses decelerate because the most money that can ever be lost is the initial premium paid. The position is negative theta because of the time value decay effect. It is positive vega and rho because the call will become more valuable if volatility increases or interest rates rise.
Signs of the ‘Greeks’ for basic option strategies

The change in the value of an option for a small change in the price of the underlying is measured by delta. Delta is the slope or tangent on the option price curve. It is also the hedge ratio, the number the trader uses to decide how much of the underlying to trade to manage the risk on an option position. Delta is not a constant and is most unstable when an option is at-the-money and approaching expiry. Theta measures the change in the value of an option as time elapses.
It is negative for bought option contracts. Vega or kappa measures the change in the value of an option for a given change in volatility. It is positive for bought calls and puts. Rho measures the sensitivity of the option value to a change in interest rates. It is positive for long calls and negative for long puts.
The first-order ‘Greeks’ delta, Vega, theta and rho are partial derivatives of the option pricing model. This means that they assume that only one factor used to determine the value of an option is changed, and the other inputs to the model are kept constant.
Gamma is a ‘second order’ Greek: it measures the change in one of the first-order Greeks (the delta) for a small change in the spot price of the underlying